duckが送るBeginnersCTF2019 BitFlip（Crypto)の解説 Not初心者向け

どうもduckです。最近は仕事とctfしかしてません。ブログタイトル「CTFと共に生きる」とかにしません？
今回はCryptoのラスボスBitFlipです。いろんな方のwriteupを読ませていただきましたが、使われている数学について解説しているwriteupはないんじゃないか？
私がやるしかないな！（需要？なにそれおいしいの？）
まずはもらったコードから

f:id:falconctf:20190529191346p:plain — BitFlip

これを解析すると以下の操作が行われていることがわかります。

f:id:falconctf:20190529192334p:plain — Flip

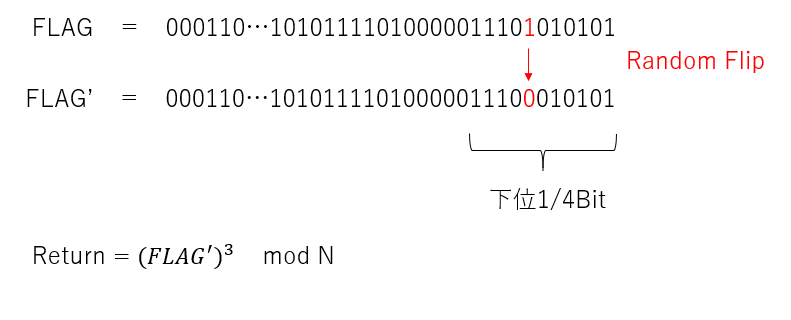
まず最初に思いつく方法はブルートフォースです。
が、美しくないうえ、サーバーから全てのReturnの情報を得なければならないので割愛します。
（ついでに言えば途中で運営側からBitFlipのサーバーにアクセスしすぎだよ自重しろというお達しもありました。つまりはブルートフォース以外の方法があるはず）
気になる方はこちらの方のWriteupを見るとよいです。
SECCON Beginners CTF 2019 - Qiita

さてここから数学のお話。
今回私の記事の中では

$f_n = FLAGのNビット目を反転した値$ (ただし1番下位のbitを０bitとします)
$f= FLAG$
$C_n = (f_n)^3 mod N$ （サーバーから返ってくる値）

として話を進めます。
$f_n = f \pm 2 ^n$ となることにも注意しておきます。(Flipが0→1のときは＋、1→0のときは-)
また、書くのが面倒なのでこれ以降 $mod N$ と書くのをやめます。適宜置き換えてください。

まず、サーバーにアクセスして
$C_n \neq C_m$ となる $C_n ,C_m$ をゲットしましょう。よほど運が悪くなければ２回でゲットできます。
もちろんこの段階ではどのビットが反転されたのかわかりませんのでn,mは不明です。

ーーーーー
目標は、平文が線形関係であるときに用いることができるFranklin-Reiter Related Message Attackを行うことです。
$m_1 = a * m_2 + b$ と表せるとき、
$c_1 = m_1 ^ e mod n$
$c_2 = m_2 ^e mod n$
の暗号文 $c_1,c_2$ と公開鍵 $e,n$ がわかれば、平文 $m_1,m_2$ を求められることを使います。
まあ後でもう少しだけ解説します。
ーーーーー

1.Coppersmith’s Short Pad Attackする
$f_n - f_m = \pm2^n \mp 2^m$ でありこれを $s$ とおきます。
そうすると
$C_n = (f_m + s) ^ 3$ 　...①
$C_m = f_m ^ 3$ 　　...②
と表せます。
このsさえ求まればFranklin-Reiter Related Message Attackが使える形になります。

ここで
$P(x) = C_n - (x + s) ^ 3$
$Q(x) = C_m - x^ 3$ の多項式を考えます。( $f_m$ を未知数xに置き換えただけ)
$P(x)=0,Q(x)=0$ の解は $f_m$ を含むことは明らかです。（つまり共通解をもつ）

この性質から、sを求めるのに終結式を使います。（終結式の定義については割愛します。終結式の定義といくつかの性質 | 高校数学の美しい物語）
終結式は共通解をもつ二つの多項式に対しては０になるという性質を持ちます。
つまり $P(x),Q(x)$ から終結式を計算して、それが０になることからｓを求めます。

終結式の計算にはシルベスター行列の行列式を使います。(終結式の定義といくつかの性質 | 高校数学の美しい物語)
今回の場合は以下のようになります。
$\begin{vmatrix} 1 & 3s & 3s^2 & s^3-C_n & 0 & 0\\ 0 & 1 & 3s & 3s^2 & s^3 - C_n & 0 \\ 0 & 0 & 1 & 3s & 3s^2 & s ^3 - C_n\\ 1 & 0 & 0 & -C_m & 0 & 0 \\ 0 & 1 & 0 & 0 & -C_m & 0 \\ 0 & 0 & 1 & 0 & 0 & -C_m \end{vmatrix}$

~~こっから先は手計算では無理だ。~~
アホなので手計算でシルベスターの行列式計算しました。
$(s^3 + C_m - C_n) ^ 3 - 27 * s^3 * C_m (s^3 + C_m - C_n) + 27 * s^3 * C_m ^2 + 27 s^6 * C_m$
sの大きさに注意しつつプログラムに投げましょう。後でやります。（おい）Sagemathがpythonライクでおすすめだった気がします。
mathematicaとかフリーで使えたっけ？使えるならそっちでも。
sのサイズが大きすぎるため、このままプログラムに投げるには $C_n,C_m$ としていい値が来ないと計算無理です。
何回も問題サーバーにアクセスして解けるパターンを待ってもいいですが、今回はわかってる情報からsがある程度絞り込めるのでそれを利用します。
$s = \pm2^n \mp 2^m$ の形なのがわかっているので、これを使い $\frac{(max(n))*max(n-1)} {2}*4$ 回くらい終結式を計算すればよいことがわかります。
今回はmax(n)として250くらいを取りました。
このmax(n)は実験中にサーバーサクセスを繰り返してたときに推測した値です。
これでSagemathをつかわなくともsが求まります。
以下くそコード。

N = 82212154608576254900096226483113810717974464677637469172151624370076874445177909757467220517368961706061745548693538272183076941444005809369433342423449908965735182462388415108238954782902658438063972198394192220357503336925109727386083951661191494159560430569334665763264352163167121773914831172831824145331
e = 3
#max(n)
nm = 250
C1 = 19668512534871703818804721058464184088540192186216654188589585883263154008964228350399514299852538811337835790238510703474647742023573370430287373841543674974547734434937124159068497046659147350241364684829208188803795307462087810637640642350674397153687260268727800582499681256385837706667398671154929189579
C2 = 44939803625275977251911534717835431979049524856461188120868461571121976859707514547338914366715426490130522458001402249990220314314873155256383447002643583335186960138112746521599509022925369612324695641201278318699732590955718931066187237603506202339345820308234883558809220466506231185260966657450242854347

#2べきを先にリストに格納
list2 = []
t = 1
ans = 0
i = 0
while i <= nm:
    list2.append(t)
    t = t * 2
    t = t % N
    i += 1

#sを表示する
def result(s,n,m,l):
    print(s,n,m,l)
    ans = s

#ブルートフォース
for n in range(nm):
    for m in range(nm)[n+1:nm]:
        #2^m + 2^n or 2^m - 2^n
        s = (list2[m] + list2[n]) % N
        if solve(s):
            result(s,n,m,0)
        elif solve(-s):
            result(s,n,m,1)
        #2^m - 2^n or 2^n - 2^m
        s = (list2[m] - list2[n]) % N
        if solve(s):
            result(s,n,m,2)
        elif solve(-s):
            result(s,n,m,3)

solve関数が消えていますが、うえで示した終結式に代入して、＝ $０$ ならTrue　, $\neq 0$ ならFalseを返すだけの関数です。
結果はこちら
383123885216472214589586756787577295904680382499389440 42 178 3

今回のケースでは
FLAGの42bit目が０→１反転したものと、178bit目が1→０反転したものであることがわかりました。
まあ $s=383123885216472214589586756787577295904680382499389440$ さえ知ってれば大体OKですが。

2．Franklin-Reiter Related Message Attackする
$C_n = (f_m + s) ^ 3$ 　...①
$C_m = f_m ^ 3$ 　　...②
のsが1で求まったとします。
$s=383123885216472214589586756787577295904680382499389440$ です。
この時 $f_m$ は $gcd(P(x),Q(x))$ で求まります。（雑）

もうちょっとだけ解説を加えます。
$gcd(P(x),Q(x))$ は多項式版ユークリッドの互除法をして、最大公約多項式を求めろということです。
整数のユークリッドの互除法とおんなじです。そしたら答えがわかります。（雑）

例を挙げます。
$p = x ^2 - 1$
$q = x ^ 3 - 1$
の最大公約単項式を求めてみましょう。
頑張ってユークリッドの互除法をすると以下のようになります。
$gcd(p,q)=x-1$
ということは
$p=(x-1)*(なんかの１次式)$
$q=(x-1)*(なんかの2次式)$
となっていることを意味します。
つまり共通因数がわかったってことだ！！
これ見たら $p,q$ の共通解はどう見ても１やんけ！ってなわけですね。

$P(x),Q(x)$ は共通解 $f_m$ を持つことがわかっているので、 $gcd(P(x),Q(x))$ は必ず１ではない多項式です。
ほとんどの場合で、それは1次多項式であり $gcd(P(x),Q(x)) = x -f_m$ となりますから $f_m$ がわかります。
（まれに $gcd(P(x),Q(x))$ が２次式以上になりますが、それを解いて $f_m$ を求めるのはかなりめんどくさいのでおとなしく $C_1,C_2$ の選択からやり直すのをおすすめします。）

実際にやってみた結果。（Sagemathを使いました。sympyだと整数環上でしかできなかったためあきらめた。）

PRx.<x> = PolynomialRing(Zmod(N))
g1 = x^e - c1
g2 = (x+s)^e - c2

while g2:
    g1, g2 = g2, g1 % g2
    print(g1.monic())

結果。
$x + 82212154592315489750110187598968636841905821953623851870053845076997511568524415687534405445330110037385522700226033733612223434284079949332614038131717774815337863135195292470488899872185912270098336585556230191588353421626879687269516794206695695261382777258681677254870347368455087826235419500816586773161$
つまり
$f_m = - 82212154592315489750110187598968636841905821953623851870053845076997511568524415687534405445330110037385522700226033733612223434284079949332614038131717774815337863135195292470488899872185912270098336585556230191588353421626879687269516794206695695261382777258681677254870347368455087826235419500816586773161$

bit反転させるのが筋ですが、もうめんどいのでこのまま復号します。

from Crypto.Util.number import bytes_to_long, getRandomInteger, getPrime,long_to_bytes

N = 82212154608576254900096226483113810717974464677637469172151624370076874445177909757467220517368961706061745548693538272183076941444005809369433342423449908965735182462388415108238954782902658438063972198394192220357503336925109727386083951661191494159560430569334665763264352163167121773914831172831824145331
m = -82212154592315489750110187598968636841905821953623851870053845076997511568524415687534405445330110037385522700226033733612223434284079949332614038131717774815337863135195292470488899872185912270098336585556230191588353421626879687269516794206695695261382777258681677254870347368455087826235419500816586773161
m = m % N

print(long_to_bytes(m))

ctf4b{b1tfl1pp1ng_1s_r3lated_m3ss4ge} DUMMYDUMMYDUMMYDUMMYDUMMYDUMMYDUMMYDUMMYDUMMYDUMMYDUMMYDUMMYDUMIYDUMMYDUMMYDUMMYDUMMY\n

反転さぼった影響で赤い部分の文字が変わってますね。（気になる人は178bit目を反転させましょう）まあもうFLAG出たしいいでしょう。
お疲れさまでした。